Ángulos inscriptos: teorema II

Todos los ángulos inscriptos que abarcan el mismo arco son congruentes.

Es claro que todos los ángulos abarcan el mismo arco, AB. El central correspondiente en todos los casos es AOB. Por lo tanto, todos los ángulos tienen una amplitud igual a la mitad de AOB y por lo tanto miden lo mismo.

 

Ángulos inscriptos: teorema I

Si ángulo inscripto abarca una semicircunferencia, entonces es recto.

Demostración:

Para la demostración debemos como teorema previo, el que dice que si un ángulo inscripto y un central abarcan el mismo arco, entonces el central es el doble del inscripto.

En nuestro caso:

El ángulo BAC es inscripto y abarca el arco BC (semicircunferencia), el ángulo BOC abarca el mismo arco y es un ángulo llano por ser un diámetro de la circunferencia.

Por lo tanto: el ángulo BAC debe ser la mitad de un ángulo llano, en consecuencia, es recto.

Observen que no importa donde se encuentra el punto A, además, es claro que si A coincide con B o con C, no se formaría un triángulo.

 

Ángulos inscriptos y centrales en una circunferencia

Trabajo de investigación de las propiedades de los ángulos inscriptos en una circunferencia, para realizar con un programa de geometrá como Geogebra o Cabri.

Extraído de Educabri

Los ángulos inscriptos en una circunferencia tienen muchas aplicaciones en geometría. En esta clase veremos qué es un ángulo inscipto en una circunferencia, sus propiedades y algunas de sus aplicaciones.

Actividades

1-1 Ángulo inscripto

• Construí una circunferencia S con centro O y radio OR.
• Marcá tres puntos A, B y C en la circunferencia (Point on object).
• Creá los segmentos AB y BC. Marcá el ángulo ABC y medilo.
• Mové el punto B por el arco AC, ¿Qué pasa con la medida del ángulo ABC?
• Colocá ahora B del otro lado del arco AC.
• ¿Qué pasó con la medida de ABC? ¿Qué relación encontrás entre las dos medidas?
  Sugerencia: mové los puntos A o C y armá una tablita con los pares de valores que vas obteniendo para distintas posiciones de A y C.
• ¿Cuánto mide el ángulo ABC cuando AC es un diámetro de la circunferencia?
  El ángulo ABC se llama inscripto en la circunferencia S. Observamos que ABC es constante mientras B se mantenga en el mismo arco.

1-2 Ángulo central

• En la figura anterior, creá los segmentos AO y OC. Marcá el ángulo AOC y medilo.
• Qué relación hay entre la medida de ABC y la de AOC. De nuevo, te sugerimos que hagas una tablita con distintos pares de valores de ABC y AOC.
  El ángulo AOC se llama ángulo central. Observamos que AOC es el doble de ABC.

1-3 Ángulo inscripto en una semicircunferencia

• ¿Cuánto mide AOC cuando AC es diámetro?
  En este caso, decimos que el ángulo ABC esta inscripto en una semicircunferencia.
• Demostrá lo que observaste en el item 7 de la actividad 1-1.
  Sugerencia: usá la actividad 1-2.

Problemas

1. Demostrar las propiedades enunciadas en las actividades 1-1 y 1-2.

Sugerencia: observando los triángulos isósceles de la figura, demostrar primero que ABC mide la mitad de AOC. Deducir que ABC es constante.

Ahora podemos resolver con más generalidad:

2. ¿Qué propiedad deben cumplir los ángulos de un cuadrilátero para que exista una circunferencia circunscripta a él?

3. Sea ABC un triángulo rectángulo en A. Sea M el punto medio de BC. Probar que MA = MB = MC.

4. Sea S una circunferencia y P un punto exterior a ella. Construir las rectas tangentes a la circunferencia, que pasan por P.

 

Ángulos inscriptos y ángulos centrales

Teorema:

Si un ángulo inscripto y un ángulo central, abarcan el mismo arco, entonces el ángulo central es el doble del ángulo inscripto.

Demostración:

La demostración la vamos a dividir en tres partes.

1ra Parte: un lado del ángulo inscripto pasa por el centro C de la circunferencia.

El triángulo OBC es isósceles: los lados CO y CB son congruentes por ser radios de la circunferencia.

Los ángulos COB y CBO son congruentes: por ser los ángulos opuestos a los lados congruentes del triángulos isósceles.

Si llamamos x al ángulo OCB tenemos que:

Por ser los ángulos interiores del triánguo OCB.

Por ser ángulos adyacentes.

Entonces tenemos que y 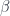son suplementos del ángulo x, por lo tanto son iguales.

Es decir:

2da Parte: el centro se encuentra dentro del ángulo inscripto.

Para comenzar la demostración debemos trazar una semirrecta auxiliar.

En el gráfico vemos que

El ángulo ACD es un ángulo central que abarca el arco AD y su correspondiente inscripto es AOC. Por lo tanto:

El ángulo DCB es un ángulo central que abarca el arco DB y su correspondiente inscripto es COB. Por lo tanto:

En consecuencia:

Por lo tanto:

3ra Parte: el centro se encuentra fuera del ángulo inscripto.

Para comenzar la demostración debemos trazar una semirrecta auxiliar.

En el gráfico observamos:

El ángulo DCB es central y abarca el arco DB, su correspondiente inscripto es COB. Por lo tanto:

El ángulo DCA es central y abarca el arco DA, su correspondiente inscripot es COA. Por lo tanto:

En consecuencia:

Por lo tanto:

 

Ángulo inscripto

Un ángulo es incripto a una circunferencia cuando su vértice pertenece a la circunferencia y sus lados son secantes a la misma.

Los lados son secantes a la circunferencia porque tienen dos puntos de intersección.

 

Rectas secantes: oblicuas y perpendiculares

Si dos rectas tienen un punto en común se llaman secantes.

Las rectas secantes se clasifican en oblicuas y perpendiculares.

Rectas Oblicuas

Si dos rectas tienen un punto de intersección, y forman ángulos no todos iguales, las rectas se llaman oblicuas.

Rectas Perpendiculares

Si dos rectas tienen un punto de intersección, y forman cuatro ángulos iguales, las rectas se llaman perpendiculares y los ángulos se llaman rectos.

 

Platón

En La República, Platón combina de forma maravillosa el concepto de postulado con su idea del mundo de las formas matemáticas:

«Creo que sabes que quienes se ocupan de geometría, aritmética y otros estudios similares dan por supuestos los números impares y pares, las figuras, tres clases de ángulos y otras cosas emparentadas con éstas y distintas en cada caso; las adoptan como hipótesis, procediendo igual que si las conocieran, y no se creen ya en el deber de dar ninguna explicación ni a sí mismos ni a los demás con respecto a lo que consideran como evidente para todos, y de ahí es de donde parten las sucesivas y consecuentes deducciones que le llevan finalmente a aquello cuya investigación se proponían.
¿Y no sabes también que se sirven de figuras visibles acerca de las cuales discurren, pero no pensando en ellas mismas, sino en aquello a que ellas se parecen, discurriendo, por ejemplo, acerca del cuadrado en sí y de su diagonal, pero no acerca del que ellos dibujan, e igualmente en los demás casos: y que así, las cosas modeladas y trazadas por ellos, de que son imágenes las sombras y reflejos producidos en el agua, las emplean, de modo que sean a su vez imágenes, en sus deseo de ver aquellas cosas en sí que no pueden ser vistas de otra manera sino por medio del pensamiento?»

Extraído de ¿Es Dios un matemático? de Mario Livio, página 35.

 

Ecuación continua de la recta

Si en la forma paramétrica despejamos t en ambas ecuaciones obtenemos:

igualando las expresiones nos queda la ecuación continua de la recta:

En la ecuación continua desaparece el parámetro y queda una única ecuación.

En forma general podemos escribrir la ecuación continua de la siguiente manera:

donde (c,d) son las coordenadas de un punto en la recta y son las componentes de un vector sobre la recta.

Ejercitación:

A partir del siguiente gráfico obtengan la ecuación continua de la recta que pasa por los punto A y B.

 

Ecuación paramétrica de la recta

A partir de la ecuación vectorial de una recta:

De donde obtenemos las siguientes ecuaciones, llamadas ecuaciones parámetricas de la recta.

en las cuales las coordenadas dependen de un mismo parámetro .

-.-.-.-.-.-.-.-.-.-

Siguiendo con el ejemplo dado en la ecuación vectorial, las ecuaciones paramétricas de la recta r serán:

observemos que los términos de las ecuaciones corresponden al punto y que los coeficientes del parámetro corresponden a las componentes del vector .

 

Ecuación vectorial de una recta

Supongamos que tenemos una recta r que pasa por el punto O=(2,3) y que tiene una dirección dada por el vector v de componentes (3,1).

Las coordenadas del un punto P de coordenadas (x,y) perteneciente a la recta, pueden obtenerse a partir de:

Recuerden que las componentes de un vector OP pueden obtenerse restando las coordenadas del extremo menos las coordenadas del origen P – A.

Haciendo un pasaje de términos.

Si generalizamos:

Nos queda:

Ecuación vectorial de la recta:

donde son las coordenadas de un punto cualquiera de la recta.

son las coordenadas de un punto conocido de la recta.

es un parámetro, puede tomar cualquier real.

son las componentes de un vector sobre la recta.

 

Rectas paralelas

Dos rectas que están en el mismo plano y no tienen ningún punto de intersección, se llaman rectas paralelas.

 

Ángulos consecutivos

Dos ángulos son consecutivos cuando sólo tienen un lado en común.

Los ángulos α y β son consecutivos, la semirrecta OC es lo único que tienen en común.

 

Ángulo

Dos rectas que tienen un punto de intersección, dividen al plano en cuatro regiones, cada uno de ellas recibe el nombre de ángulo. El punto de intersección es el vértice del ángulo, y las semirrectas que forman los bordes de la región se llaman lados del ángulo.

En el gráfico anterior las rectas r y s tienen el punto O en común, pintamos uno de los ángulos formados y lo nombramos con la letra griega α.

También podemos nombrar un ángulo a partir de tres puntos, el vértice y dos puntos pertenecientes a cada uno de los lados.

El ángulo alfa tiene vértice O y sus lados a y b pasan por los puntos A y B respectivamente, puede escribirse poniendo un símbolo parecido a un sombrero sobre el vértice e indicando los puntos por donde pasan los lados, como en la figura. Es decir, al ángulo alfa lo podemos nombrar como el ángulo AOB, sobreentendiendo que en el medio de los tres puntos se encuentra el vértice.

 

Semiplano

Si tenemos un plano α y una recta en ese plano, el plano queda dividido en dos partes.

Cada una de esas partes recibe el nombre de semiplano de borde r.

Para indicar el semiplano que queremos tener en cuenta, determinamos un punto en dicho semiplano.

En el gráfico al semiplano sombreado lo llamaríamos semiplano de borde r, que pasa por el punto P.

En símbolos Spl(r,P)

 

Segmentos congruentes

Dos segmentos son congruentes cuando superpuestos sus extremos coinciden.

Para construir segmentos congruentes utilizaremos un compás.

Supongamos que queremos construir un segmento congruente al segmento AB pero con origen en el punto C y contenido en la semirrecta s.

Con el compás tomamos la distancia entre los puntos A y B, haciendo centro en A y con el extremo del lápiz en B.

Luego, manteniendo fija la amplitud del compás, hacemos centro en C y trazamos un arco que corte a la semirrecta s.

Marcamos el punto de intersección, en este caso lo llamamos D.

AB = CD

 

Segmento

Si consideramos una recta r y en ella dos puntos distintos A, B, llamaremos segmento de extremos A y B, al conjunto formado por los puntos que están entre A y B.

 

Semirrectas opuestas

Dos semirrectas son opuestas si están en la misma recta y lo único que tienen en común es el origen.

Las semirrectas OA y OB son opuestas, O (el origen de ambas) es el punto en común.

 

Semirrecta

Si consideramos una recta r y un punto O en la misma, la recta queda dividida en dos partes. Cada una de esas partes, junto con el punto O, recibe el nombre de semirrecta de origen O.

Para nombrarlas marcamos el punto A y un punto B en cada una de las partes.

Para denotar la semirrecta de origen O que pasa por A escribimos:

Una recta se prolonga indefinidamente a lo largo de sus dos sentidos, sin embargo, una semirrecta sólo lo hace en uno de sus sentidos, por eso se dice que la semirrecta tiene principio (el origen) pero no tiene fin.

 

Nuestro primer teorema

Teorema: por una recta y por un punto que no pertenece a la misma, pasa un único plano.

Demostración: Recuerden que sólo podemos utilizar los conceptos y los axiomas vistos anteriormente para la demostración.

Paso 1: El enunciado del teorema tiene dos partes, en la primera nos dice con los conocimientos que contamos, nos enmarca la situación de la cual debemos partir (Hipótesis); la segunda parte del teorema nos da la conclusión o sea a lo que debemos llegar (Tesis).

Para este teorema en particular la hipótesis es que tenemos una recta y un punto que no está en la recta, ese debe ser nuestro punto de partida; la tesis nos indica que por esos dos objetos, en esas condiciones, pasa un único plano.

Paso 2: Tenemos una recta que llamaremos “r” y un punto fuera de ella que llamaremos “C”. Por el axioma 3 sabemos que r tiene infinitos puntos, a dos de esos puntos los llamaremos A y B. Lógicamente nos encontramos que tenemos tres puntos A, B y C que no estan alineados, pues C no está en la recta que pasa por A y B. Ahora podemos usar el axioma 7 que nos dice que por A, B y C pasa un único plano al cual llamaremos α.  Nos queda utilizar el axioma 8 el cual nos asegura que la recta r, que contiene a los puntos A y B, también pertenece al plano  α.

Conclusión: la recta r y el punto C pertenecen a un único plano que llamamos α.

 

Axiomas básicos de la geometría

Además de los conceptos primitivos para construir el conocimiento geométrico, necesitamos de ciertos postulados que no necesitan demostración por resultar evidentes, a dichos postulados los llamaremos axiomas. Los axiomas también resultan ser entonces el punto de partida, todas los otros postulados que vayamos construyendo necesitarán demostración, es decir que, utilizaremos la lógica junto con los conceptos primitivos y los axiomas para validarlos. Estos nuevos postulados recibirán el nombre de teoremas, y entonces ellos pueden usarse para las demostraciones de los siguientes postulados o propiedades.

Axiomas

Un “axioma” es una proposición evidente por sí misma y por lo tanto no necesita demostración.

Los axiomas y los conceptos primitivos son la base fundamental de la geometría.

Axiomas básicos

1-    El espacio tiene infinitos puntos, rectas y planos.

2-    El plano tiene infinitos puntos y rectas.

3-     La recta tiene infinitos puntos.

4-    Por un punto pasan infinitas rectas.

5-    Por una recta pasan infinitos planos.

6-    Por dos puntos pasa una única recta.

7-    Por tres puntos no alineados pasa un único plano.

En este caso debemos aclarar que significa alineados. Tres puntos están alineados si pertenece a una misma recta.

8-    Si dos puntos pertenecen a un plano, la recta que pasa por esos dos puntos también se encuentra en el mismo plano.